ものづくりドットコムの熊坂です。
年が変わったと思ったらもう半月過ぎてしまいました。油断も隙もありませんね(^^) 今年はどんな年にしますか?何をすれば良いかはだいたい皆分かっているもので、誰かではなく自分でブレーキを踏んでいるだけなんですよね。「それ」を実行すれば、新たな道が拓けますよ。
想いを新たに、挑戦していきましょう!
さてものづくり革新のキーワードを毎回ひとつずつ紹介しており、今回は前回に引き続き「タグチメソッド」ですが、そこで使われる直交表についてお話します。
いっぺんにたくさんの因子を評価する
前回までにタグチメソッド独特の「技術評価方法」である「SN比」について説明しました。これを大きくすれば安定した≒トラブルの起きにくい技術になるのですが、そのためには設計者が自由に決められる因子=パラメータを変化させて実験することになります。
ほとんどの人は一つあるいは二つの因子を少しずつ変化させて最適値で固定し、次に他の因子を変化させて、少しずつ良い因子水準を探していきます。これを逐次実験と呼びますが、次のような問題点があります。
- 交互作用があると、実験の順番によって結果が変わる場合がある。
- 良い結果が得られても、最適組み合わせの保証がない。
- いつ目標に達するか分からない。非常に多数回の実験が必要な時がある。
ならばたくさんの因子のすべての水準組み合わせを実験すれば、このような問題は解決するわけですが、2水準で3因子:組み合わせ数23=8サンプルまでならまあ何とかなるものの、4因子24=16、5因子25=32サンプルあたりになると、現実的ではなくなってきます。
そこでタグチメソッドで採用するのが直交表という道具です。これは言ってみれば統計的な手抜き実験法です。例えば7因子を2水準で全組み合わせは27=128サンプル必要となりますが、下図1のL8(27)という直交表を使うと、たった8通りの組み合わせで7因子の各種効果を評価することが可能となります。 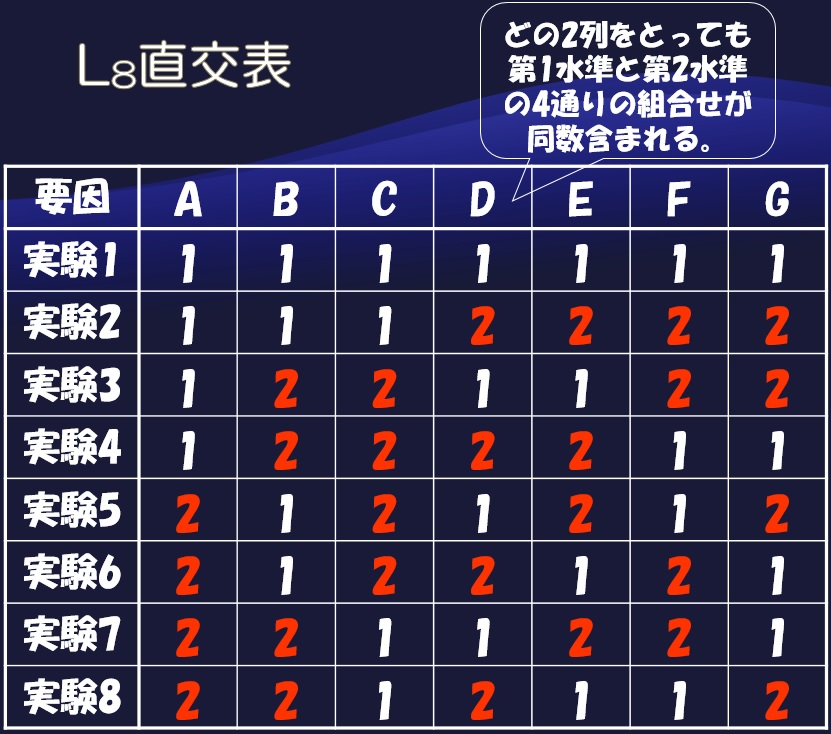
図1.L8直交表
直交表の仕組み
上の図1を良く観察しましょう。7つの因子列のどの2列を取り出しても、因子水準の組み合わせ(1,1)(1,2)(2,1)(2,2)という4種類が必ず2回ずつ現れます。それによってある因子の効果を評価する時に、第1水準4個と第2水準4個のそれぞれの実験結果の平均を比べることで、他の因子効果が相殺されて結果に影響を与えないことになり、簡単な計算で7因子の主効果が、繰り返し数4で分かってしまうのです。
ただし因子間の交互作用が大きい場合は、この理屈が正確には成り立ちません。128通りの組み合わせ中のたった8通りを実験するだけですから仕方がありません。大きな交互作用がいくつもあると、直交表を使った評価は不正確になっていきますが、もし直交表を使わず適当に実験していると、多くのサンプルを使いながらも不正確ということすら分からず、いつまでも右往左往することになります。
前節ではL8直交表を例示しましたが、他にも下表1のように3水準や多数の因子を扱えるものなどたくさんの種類があり、実験目的や内容、許される費用や期間などに応じて使い分けることになります。
表1.主な直交表の種類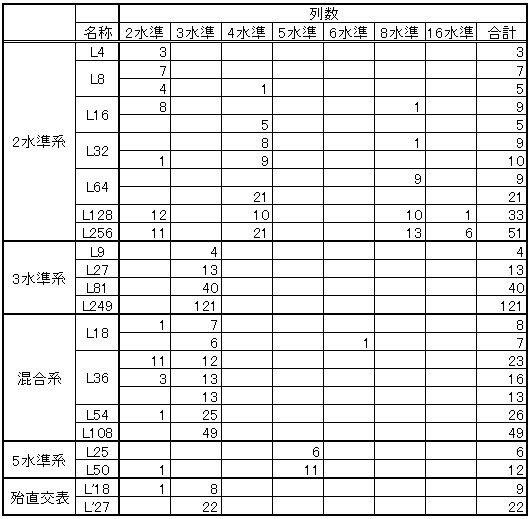
実際の利用にあたっては、4水準以上の変数の扱いや、水準間隔の考え方など多くのノウハウがあります。
パラメータ設計
前回説明した基本機能評価に、上記の直交表を組み合わせて制御因子の最適水準組み合わせを探索するのがパラメータ設計です。その構造を下図2にまとめます。
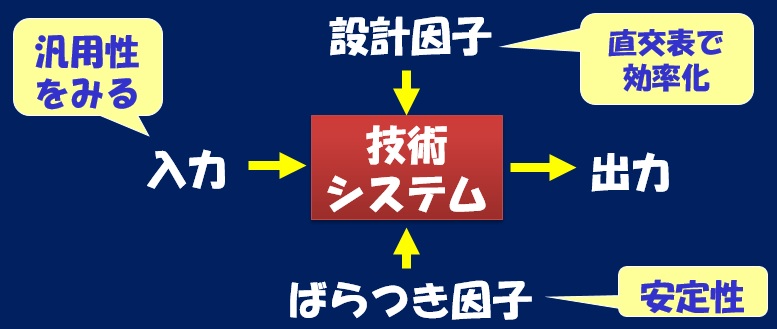
図2.技術システムとパラメータ設計の関係
その効用をまとめると次のようになります。
- 実験で意図的に特性をばらつかせる因子を加えることで、技術の良しあしを安定性によって評価し、
- 入力変化に対する出力の応答性を見ることで、技術の汎用性を確保するとともに、評価の感度を向上し、
- 直交表を使うことで多くの設計因子を一度に評価するとともに、設計因子どうしの交互作用についてもある程度の緩衝効果を発揮する。
前々回紹介したように、多くの企業がこの方法を使って高いレベルすなわち低コストで良い特性が安定的に続く技術を短期間に開発、設計するようになっています。ちょっと手強い手法ではありますがそれだけに、品質問題で窮地に追い込まれる前に習得しておきたいものです。導入にあたっては、さらに詳細な情報を入手するか、経験者の指導のもとで進めるのが早道でしょう
どうでしょう、参考になりましたか?ものづくりドットコムでは、村島繁延さんがこの分野の専門家です。不明の点やご相談はQ&Aコーナーや問い合わせフォームで質問してください。